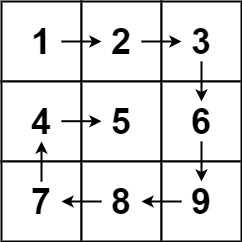
Introduction

One question called The Spiral Matrix problem puzzled me for quite some time. After studying the solution, I realized it’s not as difficult as it seems. However, I wanted to write this post to help you understand the patterns of Matrix Iteration, hope it might give you some idea.

This guide focuses on recognizing iteration patterns in matrices, enabling you to solve similar problems with ease. The same logic can also be applied to counter-clockwise traversal.

The Code

Well, let’s begin with the complete code and then break it down step by step:

#include <iostream>
#include <vector>
using namespace std;

void Matrix_Iteration(vector<vector<int>>& matrix){
    if(matrix.empty() || matrix[0].empty()){
        return;
    }
    
    int top = 0, bottom = matrix.size() - 1;
    int left = 0, right = matrix[0].size() - 1;
    
    while(top <= bottom && left <= right){
        // Go from left to right
        for(int col = left; col <= right; ++col){
            cout << matrix[top][col];
        }
        ++top;
        
        // Go from top to bottom
        for(int row = top; row <= bottom; ++row){
            cout << matrix[row][right];
        }
        --right;
        
        // Come back from right to left
        if(top <= bottom){
            for(int col = right; col >= left; --col){
                cout << matrix[bottom][col];
            }
            --bottom;
        }
        
        // Come back from bottom to top
        if(left <= right){    
            for(int row = bottom; row >= top; --row){
                cout << matrix[row][left];
            }
            ++left;
        }
    }
}

int main()
{
    vector<vector<int>> matrix = {
        {1,2,3},
        {4,5,6},
        {7,8,9}
    };
    
    Matrix_Iteration(matrix);
    return 0;
}

The Pattern Breakdown

“Wow, that’s a lot of code!” you might say. Don’t panic, we’re about to start, and please give me just 3 minutes, and you’ll walk away with no more fear for Matrix Iteration 😉!

Note: I’ll use C++ to explain the code, but the logic is the same for other languages.

1. Initialization

I won’t bother to explain this part, as it is self explanatory.

void Matrix_Iteration(vector<vector<int>>& matrix){
    //Check if the matrix is empty, they're edge cases.
    if(matrix.empty() || matrix[0].empty()){
        return;
    }
    
    //`top` and `bottom`: Control vertical movement (up and down).
    //`left` and `right`: Control horizontal movement (left and right).
    int top = 0, bottom = matrix.size() - 1;
    int left = 0, right = matrix[0].size() - 1;
}

As simple as they’re only edge cases, and variables that define the boundaries for traversal and are updated after each loop. I believe you can understand this part.

Pattern 1: Switching Between Rows and Columns

The first pattern you should notice is how the inner For loops switch between row and col, as it goes like: col -> row -> col -> row. Therefore, as long as you figure out the first one (row OR col), you can apply the rest without thinking.

In a clockwise motion, we traverse to right first, so the column is changing, and we start with column index.

//The while loop condition is self explanatory.
while(top <= bottom && left <= right){
    // Don't worry about the ending increment or decrement yet, just focus on the switch between row and col.
    for(int col = ; col  ; ++col){
    }

    for(int row = ; row  ; ++row){
    }

    for(int col = ; col  ; --col){
    }

    for(int row = ; row  ; --row){
    }
}

Pattern 2: The Constants

Let’s now focus on each individual For loop. Like I said, the only thing you should figure out, is the first For loop, and let’s do that. First move, we go from 1 -> 2 -> 3 (from left to right), and we are currently on the top row.

Spiral Matrix

// Go from left to right
for(int col = left; col <=right ; ++col){
    cout << matrix[top][col]; // `Top` is constant
}

And whatever the constant you have in the above loop, increment or decrement it accordingly to shift the boundary inward. And you’ll see how the next For Loop surpisingly start with that constant again!

for(int col = left; col <=right ; ++col){
    cout << matrix[top][col]; // Notice the `top` we had
}
++top; // Notice the `top` again

for(int row = top; row <= bottom; ++row){ // Notice the `top` again!

}

for(int col = ; col  ; --col){

}

for(int row = ; row  ; --row){

}

In summary:

The constant used in the current loopwill be decremented or incremented
The constatn will be used in next loop interation again.

So if we know this pattern, then for the 2nd for loop (goes from top to bottom along the right side), right should be used, changed and re-applied in next loop accordingly.

Attempt the pattern

for(int col = left; col <=right ; ++col){
    cout << matrix[top][col]; 
}
++top;

for(int row = top; row <= bottom; ++row){
    cout << matrix[row][right]; // See the `right` here
}
--right; // See the `right` here

for(int col = right; col >= left ; --col){ // See the `right`

}

for(int row = ; row  ; --row){

}

Apply to the rest

If this makes sense to you, let’s finish the rest of the loop.

for(int col = left; col <=right ; ++col){
    cout << matrix[top][col]; 
}
++top;

for(int row = top; row <= bottom; ++row){
    cout << matrix[row][right];
}
--right;

for(int col = right; col >= left; --col){
    cout << matrix[bottom][col];
}
--bottom;

for(int row = bottom; row >= top; --row){
    cout << matrix[row][left];
}
++left;

Pattern 3: Handling Edge Cases

The last two loops (right to left, bottom to top) require extra care to avoid out-of-bounds access. Use if statements to check whether the boundaries are still valid:

Some might be hard to recognize which variables to write for the if statement. So here is a simple trick: The if statement condition is opposite to the for loop condition.

//The last 2 loops
//Because the For Loop checks the `left` and `right`, therefore we check the if statement with `top` and `bottom`.

if(top <= bottom){
    for(int col = right; col >= left; --col){
        //code...
    }
    --bottom;
}

//Same logic. The For Loop checks the `top` and `bottom` to stay in bound, therefore we check `left` and `right`.

if(left <= right){
    for(int row = bottom; row >= top; --row){
        //code...
    }
    ++left;
}

Summary of Patterns

For Loop Order: Alternate between columns and rows.
Boundary Updates: Adjust and re-use the constant variable after each loop.
Edge Case Check: Use if statements to handle edge case, they’re opposite to the for loop.

Final Thoughts

Wola! You’ve made it! I hope this post gives you some idea on how to solve a matrix iteration. This type of question frequently appears in interviews, but a lot of time, companies just want to test your ability if you can tranverse it either clockwise or counter-clockwise.

If you have any questions, please feel free to email me. I’d be happy to help.

Happy coding! 😊

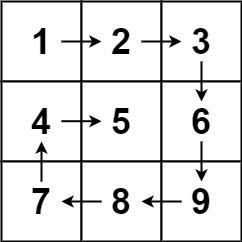
Additional Challenge: Counter-Clockwise

This is extra challenge for you to reinforce the pattern. Without further saying, let’s get started.

1. Basic Structure

void Matrix_Iteration_counter_clockwise(vector<vector<int>>& matrix){
    // Edge cases and initalization don't change.
    if(matrix.empty() || matrix[0].empty()){
        return;
    }
    
    int top = 0, bottom = matrix.size() - 1;
    int left = 0, right = matrix[0].size() - 1;

    while(top <= bottom && left <= right){

    }
}

2. The For Loops

// The iteration goes from top to bottom first (we start with row), so the pattern is row -> col -> row -> col.

for(int row = ; row  ; ++row){

}

for(int col = ; col  ; ++col){

}

for(int row = ; row  ; --row){

}

for(int col = ; col  ; --col){

}

3. The First For

First loop goes from top to bottom and stays on the left side, so we start with top.

for(int row = top; row <= bottom; ++row){
    cout << matrix[row][left];
}

Then from rule we’ve talked about, the constant from the current iteration will be updated and re-used in next iteration.

for(int row = top; row <= bottom; ++row){
    cout << matrix[row][left];
}
++left;

for(int col = left; col <= right ; ++col){

}

We’re now at the bottom of the matrix, and going from left to right.

for(int row = top; row <= bottom; ++row){
    //code...
}
//code...

for(int col = left; col <= right ; ++col){
    cout << matrix[bottom][col];
}
--bottom;

for(int row = bottom; row >= top ; --row){

}

Apply to the rest of the loops.

for(int row = top; row <= bottom; ++row){
    cout << matrix[row][left];
}
++left;

for(int col = left; col <= right ; ++col){
    cout << matrix[bottom][col];
}
--bottom;

for(int row = bottom; row >= top ; --row){
    cout << matrix[row][right];
}
--right;

4. The Last 2 Loops

Add if statement for the last 2 loops. Put the opposite variable like this:

If you see left & right in the loop, you put top & bottom in the if statement.
If you see top & bottom in the loop, you put left & right in the if statement.

if(top <= bottom){
    for(int col = right; col >= left; --col){
        //code...
    }
    //code...
}

if(left <= right){
    for(int row = bottom; row >= top; --row){
        //code...
    }
    //code...
}

5. Final Code

void Matrix_Iteration_counter_clockwise(vector<vector<int>>& matrix){
    if(matrix.empty() || matrix[0].empty()){
        return;
    }
    
    int top = 0, bottom = matrix.size() - 1;
    int left = 0, right = matrix[0].size() - 1;

    while(top <= bottom && left <= right){
        for(int row = top; row <= bottom; ++row){
            cout << matrix[row][left];
        }
        ++left;

        for(int col = left; col <= right; ++col){
            cout << matrix[bottom][col];
        }
        --bottom;

        if(left <= right){
            for(int row = bottom; row >= top; --row){
                cout << matrix[row][right];
            }
            --right;
        }

        if(top <= bottom){
            for(int col = right; col >= left; --col){
                cout << matrix[top][col];
            }
            ++top;
        }
    }
}

int main()
{
    vector<vector<int>> matrix = {
        {1,2,3},
        {4,5,6},
        {7,8,9}
    };
    
    Matrix_Iteration_counter_clockwise(matrix);
    return 0;
}

Introduction#

The Code#

The Pattern Breakdown#

1. Initialization#

Pattern 1: Switching Between Rows and Columns#

Pattern 2: The Constants#

Attempt the pattern#

Apply to the rest#

Pattern 3: Handling Edge Cases#

Summary of Patterns#

Final Thoughts#

Additional Challenge: Counter-Clockwise#

1. Basic Structure#

2. The For Loops#

3. The First For#

4. The Last 2 Loops#

5. Final Code#